How to Graph a Linear System and Estimate the Solution
USING A GRAPH TO ESTIMATE THE SOLUTION OF A SYSTEM
We can use a graph to estimate the solution of a system of equations beforesolving the system algebraically.
Example 1 :
Estimate the solution by sketching a graph of each linear function. Then solve the system algebraically. Use your estimate to judge the reasonableness of your solution.
x - 4y = 4
2x - 3y = -3
Solution :
Step 1 :
To sketch the graph of the equations, write them in slope-intercept form.
That is,
y = mx + b
x - 4y = 4
y = (1/4)x - 1
Slope = 1/4
y-intercept = -1
2x - 3y = -3
y = (2/3)x + 1
Slope = 2/3
y-intercept = 1
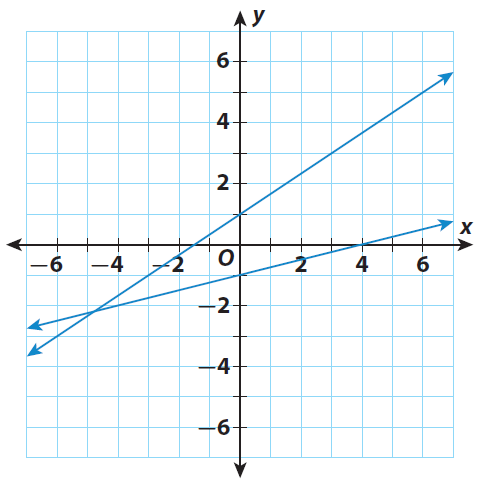
Step 2 :
Find the point of intersection of the lines. The point of intersection is near to the point (-5, -2).
Let us give (-5, -2) as our estimation to the solution of the system.
Step 3 :
Solve the system algebraically.
Select one of the equation, say x - 4y = 4 .
Solve for the variable x in terms of y.
Add 4y to both sides.
(x - 4y) + 4y = (4) + 4y
x = 4 + 4y
Step 4 :
Substitute the expression for x in the other equation and solve.
2x - 3y = -3
2(4 + 4y) - 3y = -3
8 + 8y - 3y = -3
Combine the like terms.
8 + 5y = -3
Subtract 8 from both sides.
5y = -11
Divide by 5 on both sides.
5y / 5 = -11 / 5
y = -11/5
Step 5 :
Substitute the value of y we got above (y = -11/5) into one of the equations and solve for the other variable, y.
x - 4y = 4
x - 4(-11/5) = 4
x + 44/5 = 4
Subtract 44/5 from both sides.
x = 4 - 44/5
x = -24/5
Hence, the solution of the system is (-24/5, -11/5).
Step 6 :
Use the estimate which has been made using the graph to judge the reasonableness of the solution.
-24/5 is close to -5 and -11/5 is close to -2.
So, the solution estimated from the graph (-5, -2) seems reasonable.
Example 2 :
Estimate the solution by sketching a graph of each linear function. Then solve the system algebraically. Use your estimate to judge the reasonableness of your solution.
x + y = 4
2x - y = 6
Solution :
Step 1 :
To sketch the graph of the equations, write them in slope-intercept form.
That is,
y = mx + b
x + y = 4
y = - x + 4
Slope = - 1
y-intercept = 4
2x - y = 6
y = 2x - 6
Slope = 2
y-intercept = -6
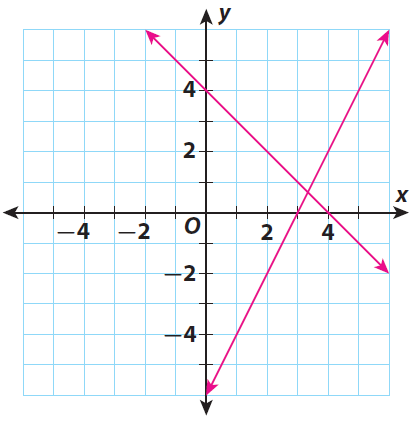
Step 2 :
Find the point of intersection of the lines. The point of intersection is near to the point (3, 1).
Let us give (3, 1) as our estimation to the solution of the system.
Step 3 :
Solve the system algebraically.
Select one of the equation, say x + y = 4 .
Solve for the variable y in terms of x.
Subtract x from both sides.
(x + y) - x = (4) - x
y = 4 - x
Step 4 :
Substitute the expression for y in the other equation and solve.
2x - y = 6
2x - (4 - x) = 6
2x - 4 + x = 6
Combine the like terms.
3x - 4 = 6
Add 4 to both sides.
3x = 10
Divide by 3 on both sides.
3x / 3 = 10 / 3
x = 10/3
Step 5 :
Substitute the value of x we got above (x = 10/3) into one of the equations and solve for the other variable, y.
x + y = 4
10/3 + y = 4
Subtract 10/3 from both sides.
y = 4 - 10/3
y = 2/3
Hence, the solution of the system is (10/3, 2/3).
Step 6 :
Use the estimate which has been made using the graph to judge the reasonableness of the solution.
10/3 is close to 3 and 2/3 is close to 1.
So, the solution estimated from the graph (3, 1) seems reasonable.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
HCF and LCM word problems
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Algebra word problems
Word problems on trains
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on unit price
Word problems on unit rate
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Double facts word problems
Trigonometry word problems
Percentage word problems
Profit and loss word problems
Markup and markdown word problems
Decimal word problems
Word problems on fractions
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Time and work word problems
Word problems on sets and venn diagrams
Word problems on ages
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Profit and loss shortcuts
Percentage shortcuts
Times table shortcuts
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Sum of all three four digit numbers formed using 0, 1, 2, 3
Sum of all three four digit numbers formed using 1, 2, 5, 6
How to Graph a Linear System and Estimate the Solution
Source: https://www.onlinemath4all.com/using-a-graph-to-estimate-the-solution-of-a-system.html